
- Upload de imagens e multimedia
- Número de Perguntas por Pesquisa
- Criando uma pesquisa a partir de um documento do Word
- Como excluir, adicionar e editar perguntas e respostas de uma pesquisa em andamento
- Blocos de Perguntas
- Randomização de Blocos
- Randomização de Perguntas
- Biblioteca de Escalas
- O que é teste monádico?
- O que são testes monádicos sequenciais?
- Suporte de extração para tipos de perguntas do seletor de imagens
- O que são testes de comparação?
- Mensagens de validação personalizadas
- Construindo pesquisas com o QxBot
- Extraktionsunterstützung para Fragetypen mit Bildauswahl
- Opções de visualização da pesquisa
- Edição e Colaboração em Pesquisas 2025 - FAQ
- Testing Send
- Add Questions From a Document
- Perguntas básicas
- Tipos de perguntas avançadas
- Múltipla escolha
- Caixa de texto
- Matriz de escala com múltiplos pontos
- Ranking
- Classificação com emoji
- Imagem
- Data e Hora
- Pergunta Re-CAPTCHA
- Satisfação do cliente: NPS - Net Promoter Score
- Pergunta Van Westendorp - pergunta sobre sensibilidade ao preço
- Choice modelling questions
- Matriz Lado a Lado
- Tipo de Pergunta Homúnculo
- Opções de resposta preditiva
- Questões de conteúdo estático
- Múltipla escolha: selecionar uma opção
- Múltipla escolha: Selecionar vários
- Pergunta com cronômetro de página
- Informações de contato
- Pergunta de matriz com múltipla seleção
- Pergunta com matriz de planilha
- Classificação com cartões - arrastar e soltar
- Matriz Flexível - Como fazer?
- Barra deslizante de texto
- Perguntas de classificação: curtir e smiley face
- Pergunta arrastar e soltar
- Matriz bipolar - controle deslizante
- Perguntas de matriz bipolar e likert
- Gabor Granger
- Assinatura Digital Verificada
- Classificação com estrelas
- Pergunta de Divulgação nas Redes Sociais
- Attach Upload File Question
- Constant Sum Question
- Informações de vídeo
- Conexão de plataforma
- Recrutamento de Comunidades
- Pergunta de classificação: vídeo TubePulse ™
- Classificação de cartão aberto
- Mapas - Tipo de Pergunta
- LiveCast
- Tipo de resposta e layout
- Reordenar Perguntas
- Question tips
- Exibição de caixa de texto
- Configurações de texto aberto
- Adicionando a opção Outro
- Configurações de matriz
- Configurações de avaliação de imagem
- Opções de escala
- Configurações de Soma Constante
- Definindo respostas padrão
- Validação de opção exclusiva para perguntas de múltipla escolha
- Como fazer uma pergunta obrigatória
- Configurações de validação
- Remove validation message
- Separadores de perguntas
- Códigos de pergunta
- Quebra de página
- Texto de introdução com caixa de seleção de aceitação
- Validação RegEx
- Biblioteca de Perguntas
- Incorporar vídeo - Como fazer
- Posição inicial do controle deslizante
- Alternância na Exibição das Respostas
- Matrix - foco automático
- Validações de texto
- Configurações de entrada numérica - planilha
- Grupos de resposta [versão BETA]
- Formato de moeda do separador decimal
- Permitir vários arquivos - tipo de pergunta anexar/carregar
- tipo-de-teclado-de-entrada-de-texto
- Mergulho profundo
- Randomização de respostas
- Alternate colors
- Análise Conjunta - FAQ sobre Melhores Práticas de Implementação
- Limites para arquivos de imagem/multimídia
- Conceitos Proibidos em Conjoint
- Hidden Questions
- Add logo to survey
- Customização de temas
- Configurações de exibição da pesquisa
- Avanço automático da pesquisa
- Barra de progresso - Como fazer?
- Opções de numeração automática de perguntas
- Enabling social network toolbar
- Browser Title
- Print or download survey
- Botões de navegação de pesquisa
- Acessibilidade - Conformidade 508
- Back and Exit Navigation Buttons
- Modo Foco
- Layout da pesquisa
- Layout da pesquisa - modo visual
- Integração com televisão
- URL do espaço de trabalho
- Layout Clássico
- Telly Integration
- Ramificação ou lógica de pulo
- Ramificação composta
- Ramificação composta
- Controle de cotas
- Texto dinâmico/comentários
- Lógica de extração
- Mostrar/ocultar perguntas
- Lógica dinâmica de exibição/ocultação
- Lógica de pontuação
- NPS - Net promoter score
- Texto de tubulação
- Pesquisa em cadeia
- Looping - como fazer
- Ramificação para encerrar a pesquisa
- Operadores de comparação / Operadores lógicos
- Lógica N de M selecionada
- Referência Lógica da Sintaxe com JavaScript
- Fluxo em bloco
- Loop de bloco
- Referência de sintaxe do motor de pontuação
- Sempre extrair e nunca extrair a lógica
- Matrix Extraction
- Extração Bloqueada
- Atualização dinâmica de variável personalizada
- Randomização Avançada
- Exemplos de scripts personalizados
- Custom Scripting
- Survey Logic Builder - AI
- Configurações da pesquisa
- Salvar e Continuar Depois
- Desabilitar respostas múltiplas
- Fechar ou desativar a pesquisa
- Admin confirmation email
- Alertas de ação
- Tempo limite da pesquisa / Tempo limite da sessão
- Opções de Finalização de Pesquisas | QuestionPro
- Relatório Spotlight
- Imprimir respostas da pesquisa
- Pesquisar e substituir
- Survey Timer
- Permite múltiplos entrevistados da mesma máquina?
- Configurações de tamanho de entrada de texto
- Notificações - E-mail de Confirmação do Administrador
- Data e hora de fechamento da pesquisa
- Dados de localização do respondente
- Modo de revisão
- Revise, edite e imprima respostas
- Codificação geográfica
- Barra de Progresso Clássica
- Response Quota
- verificação de idade
- Opções de pesquisa | Ferramentas
- Copy survey
- Edição de pesquisas compartilhadas
- Sharing survey
- Pastas - Organizar Pesquisas
- Procurando por uma pesquisa em minha conta
- Compartilhamento de lista de e-mail
- Registos de auditoria do sistema
- Pesquisa de Compartilhamento
- Compartilhamento e Colaboração em Pesquisas
- Versões da Pesquisa
- Elabore e publique pesquisas
- Tipos de Autentificação
- Pesquisa global com proteção por senha
- Autenticação usando apenas convites por e-mail
- E-mail de pesquisa e proteção por senha
- Participant ID authentication
- Username/password authentication
- SSL security
- Authentication using Facebook login
- Autenticação usando login único
- URLs de mídia criptografados
- Live survey URL
- URLs de Pesquisa Personalizadas
- Criando convite da pesquisa por email
- Fusão de correio e personalização de e-mails
- Configurações de convites por e-mail
- Filtro de lista de e-mails
- Enviando lembretes de pesquisa
- Lote de exportação para distribuição externa
- Status atual do e-mail
- Spam index
- Enviar convite para responder à pesquisa via SMS
- Pesquisas por telefone e papel
- Adicionando respostas manualmente | Pesquisas em papel | Pesquisas por telefone
- Preços de mensagem SMS
- Incorporar Pergunta no E-mail
- Excluindo listas de e-mail
- Distribuição de pesquisa multilíngue
- SMTP
- Configurar o endereço de e-mail de resposta para os convites de pesquisa enviados via QuestionPro
- Autenticação de domínio
- Solução de problemas de entrega de e-mail
- QR Code
- Email Delivery and Deliverability
- App offline - Temas
- Loop de pesquisa
- Usando o aplicativo móvel QuestionPro
- Modo Quiosque
- Sincronizar os dados do aplicativo
- Revise a resposta / imprima o pdf no aplicativo offline
- Auditoria de campo e dispositivo
- Variáveis de dispositivo offline
- Sincronizar respostas manualmente
- Hardware do dispositivo
- Detecção facial no modo quiosque
- Texto para fala
- Notificação Push
- Aplicativo off-line – práticas recomendadas
- Dashboard da pesquisa
- Overall participant statistics
- Dropout analysis
- Banner tables
- Análise TURF
- Trend analysis
- Análise de correlação
- Relatório de comparação
- O que é a análise de GAP/Lacunas?
- Mean calculation
- Weighted mean
- Análise Spider Chart
- Análise de Cluster
- Filtros do painel
- Datapad
- Dashboard - Opções de download
- Teste de imagem HotSpot
- Heatmap Analysis
- Ordem de classificação ponderada
- Opções de resposta de agrupamento de tabulação cruzada
- Teste A/B em pesquisas QuestionPro
- Qualidade de dados
- A qualidade dos dados termina
- Gráfico de mapa de calor para perguntas do tipo matriz
- teste-de-proporções-de-coluna
- Identificador de resposta
- Análise de alcance TURF
- Edição em Massa de Respostas
- Ponderação e balanceamento
- Designs de Análise Conjunta
- Cálculo dos valores de utilidade na análise de escolha discreta do Conjoint
- Análise Conjunta - Cálculos / Metodologia
- Análise Conjunta - Importância dos Atributos
- Análise Conjunta – Perfis
- Simulador de Segmentação de Mercado
- Análise Conjunta – Valor da Marca
- Escalonamento de Diferença Máxima | Max-Diff
- Configurações da Maxdiff
- Análise MaxDiff Ancorada
- Escala Max Diff - Perguntas Frequentes
- Resultados de interpretação de MaxDiff
- Envio automático de relatórios por e-mail
- Qualidade de dados - respostas padronizadas
- Qualidade de dados - palavras sem sentido
- Import external data
- Central de download
- Consolidate report
- Delete survey data
- Qualidade de dados - todas as caixas de seleção selecionadas
- Exportando dados para Word ou PowerPoint
- Agendar relatórios - Como fazer?
- Datapad
- Grupo de Notificação
- Mesclar dados 2.0
- Detecção de Plágio
- ip-based-location-tracking
- SPSS Export
- Nome da variável SPSS
- Unselected Checkbox Representation
- Update user details
- Como atualizar o fuso horário
- Business units
- Adicionar Usuários
- Usage dashboard
- Single user license
- License restrictions
- Software support package
- E-mail de boas-vindas
- Funções e permissões do usuário
- Adicionar usuários em massa
- Verificação de conta usando autenticação de dois fatores (verificação em 2 etapas)
- Acesso à rede
- Alterando a propriedade da pesquisa
- Não foi possível acessar o suporte por chat
- Navegando pelos produtos QuestionPro
- Troubleshooting login issues
- Agency Partnership Referral Program
- Response Limits
- CAN-SPAM
- Regulamento Geral de Proteção de Dados (GDPR)
- SOC 2 Segurança
- Respondent anonymity assurance
- Security
- Conformidade com a Lei de Privacidade do Consumidor da Califórnia (CCPA)
- GDPR - Direito de ser esquecido
- GDPR: solicitação de direitos de dados
- Declaração de acessibilidade do QuestionPro
- Centro de dados
- Strong Password
- Automated deletion of data
Análise Conjunta – Perfis
Perfis em um tipo de pergunta de Análise Conjunta são diferentes configurações que são apresentadas aos respondentes. Cada perfil é uma combinação de diferentes níveis de vários atributos (Por exemplo, Marca, Custo, Recursos). Ao avaliar esses perfis, os respondentes revelam suas preferências e trade-offs, permitindo que os pesquisadores estimem a importância relativa de cada atributo e seus níveis na influência da escolha do consumidor.
Com a QuestionPro, você pode acessar Perfis em um tipo de pergunta de Análise Conjunta como mostrado abaixo: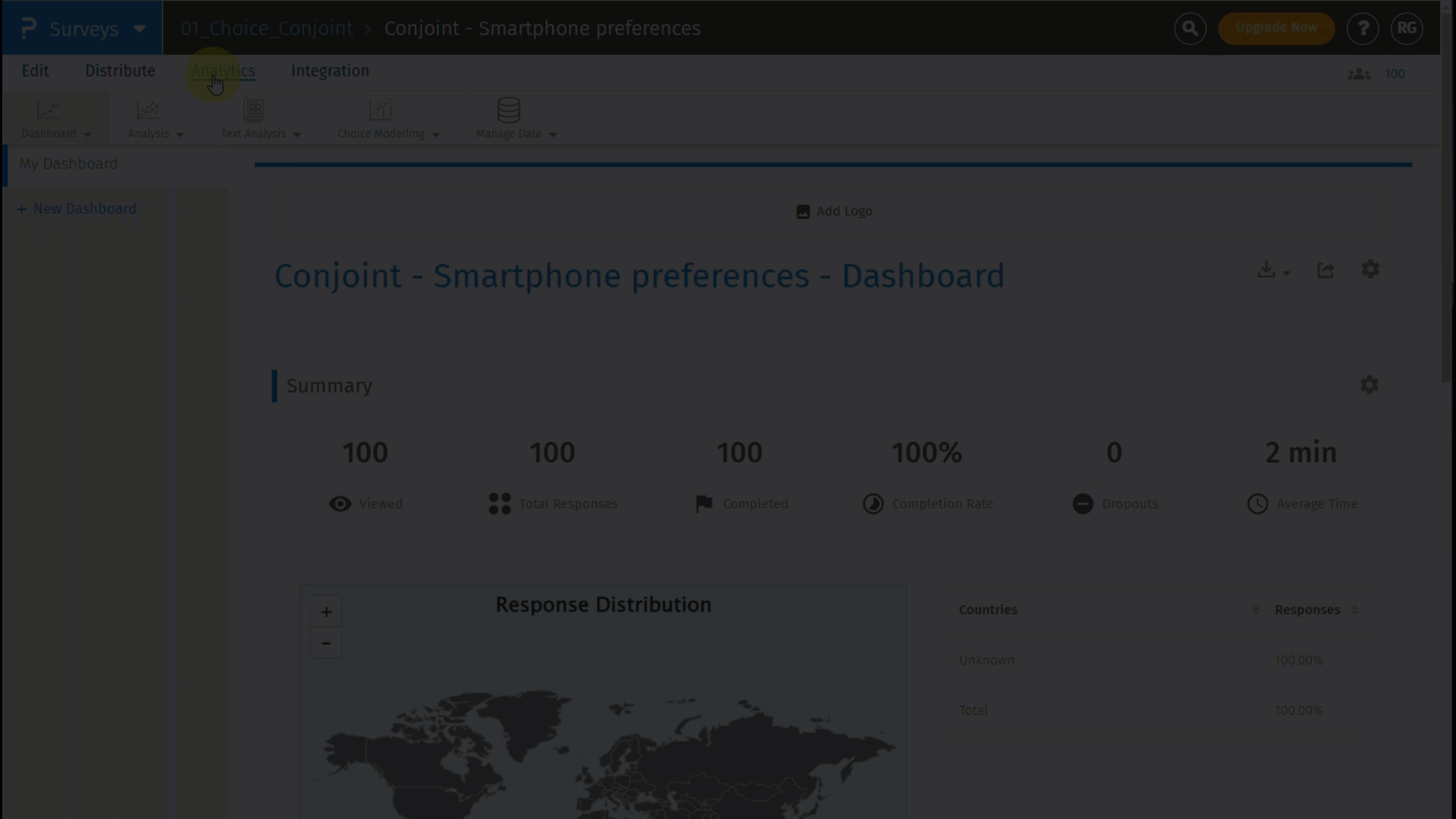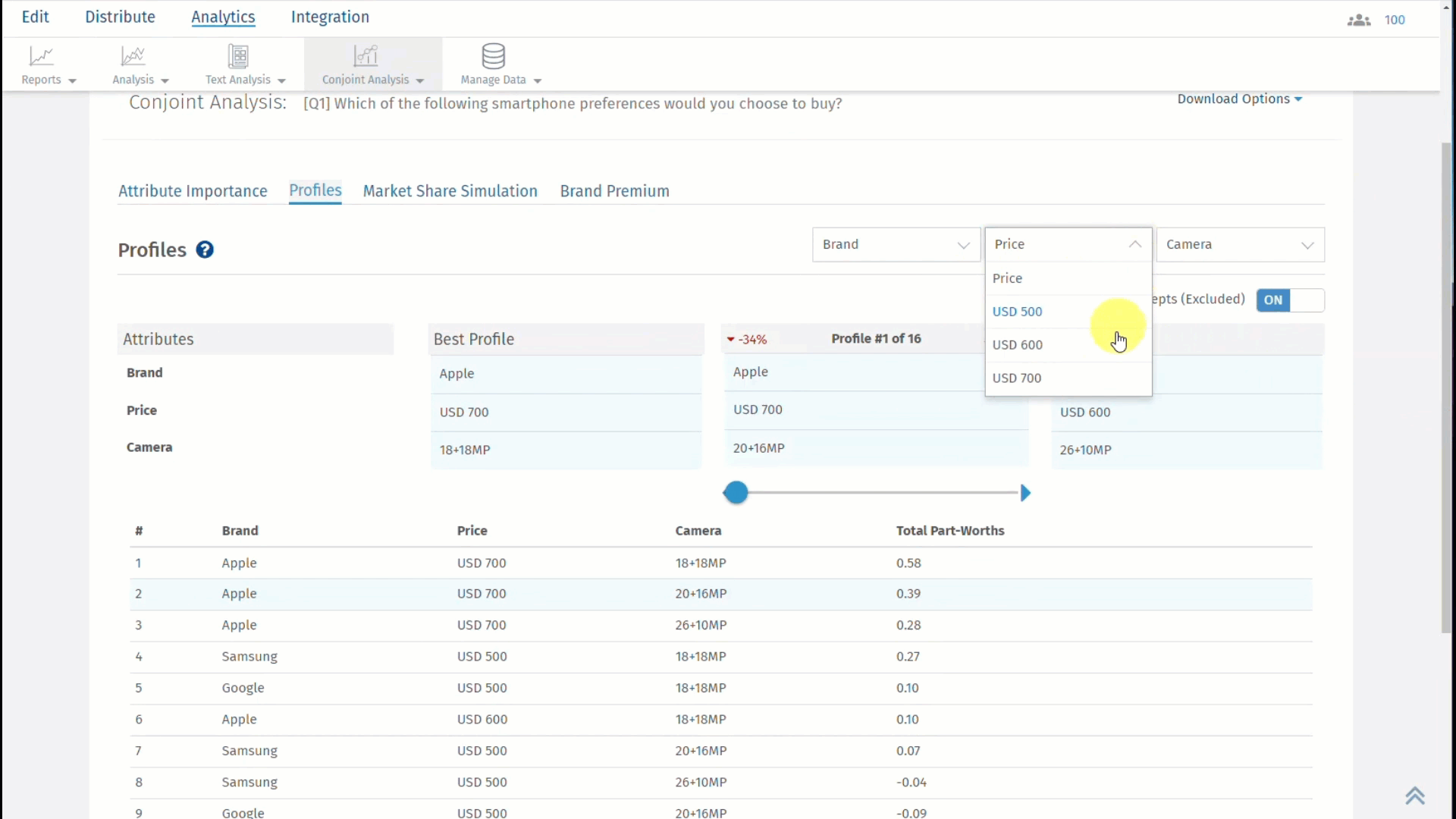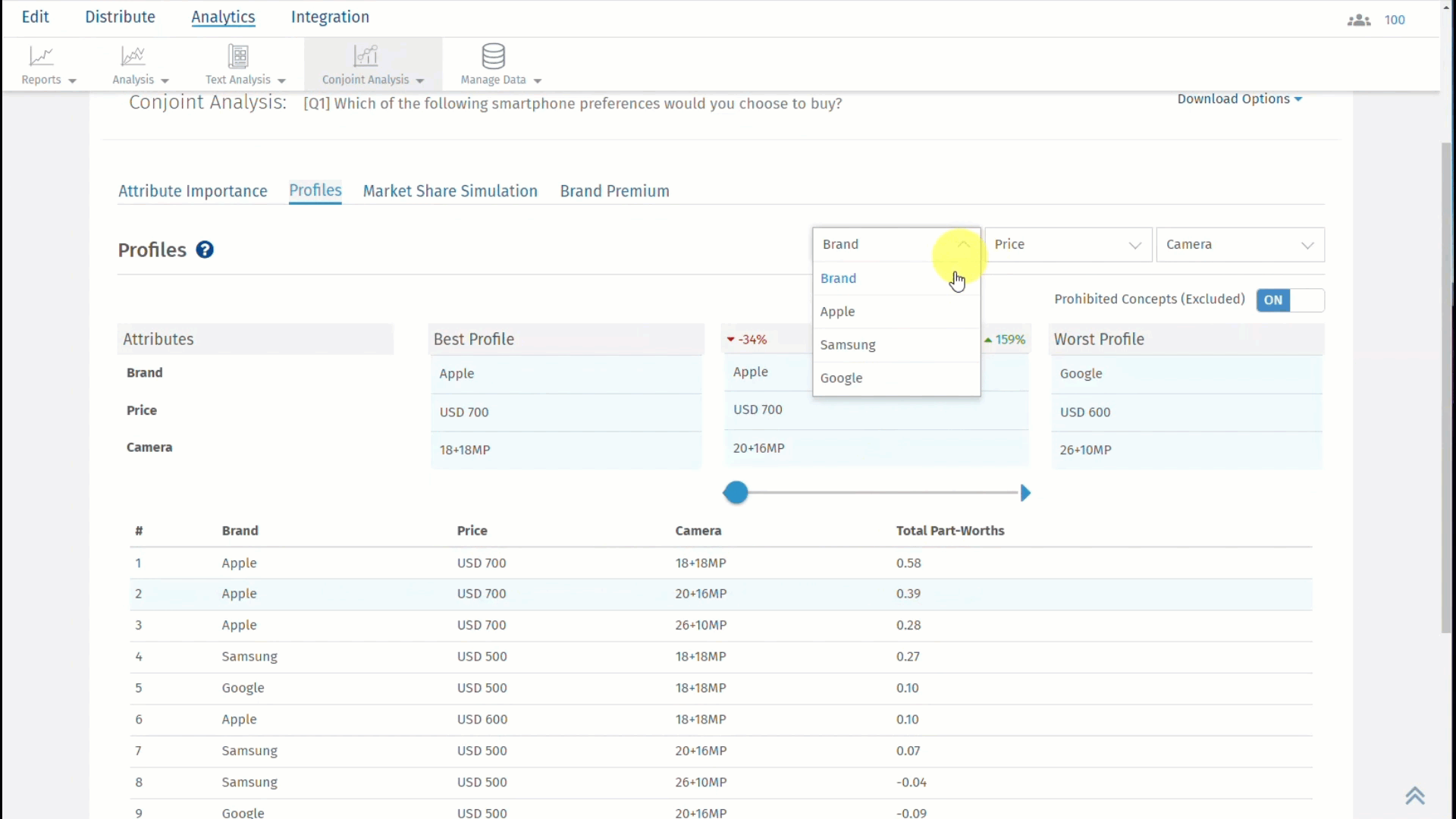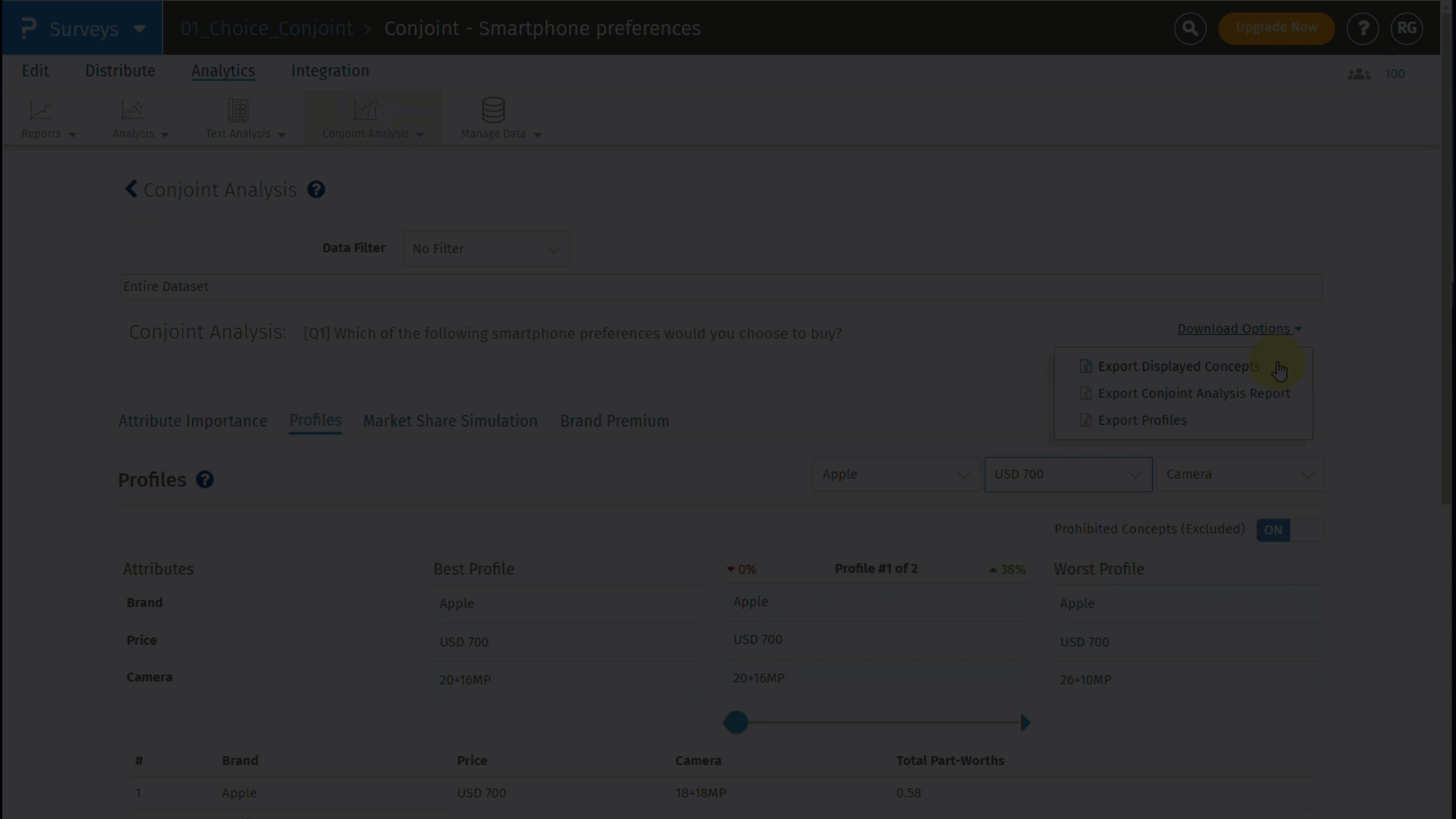
Clique em Análise
 Vá para:
Modelagem de Escolha » Análise Conjunta
Vá para:
Modelagem de Escolha » Análise Conjunta
 Selecione a pergunta para a qual a análise é necessária e clique em Próximo Passo
Selecione a pergunta para a qual a análise é necessária e clique em Próximo Passo
 Clique na segunda aba, que é Perfis e os resultados serão exibidos como mostrado abaixo:
Clique na segunda aba, que é Perfis e os resultados serão exibidos como mostrado abaixo:
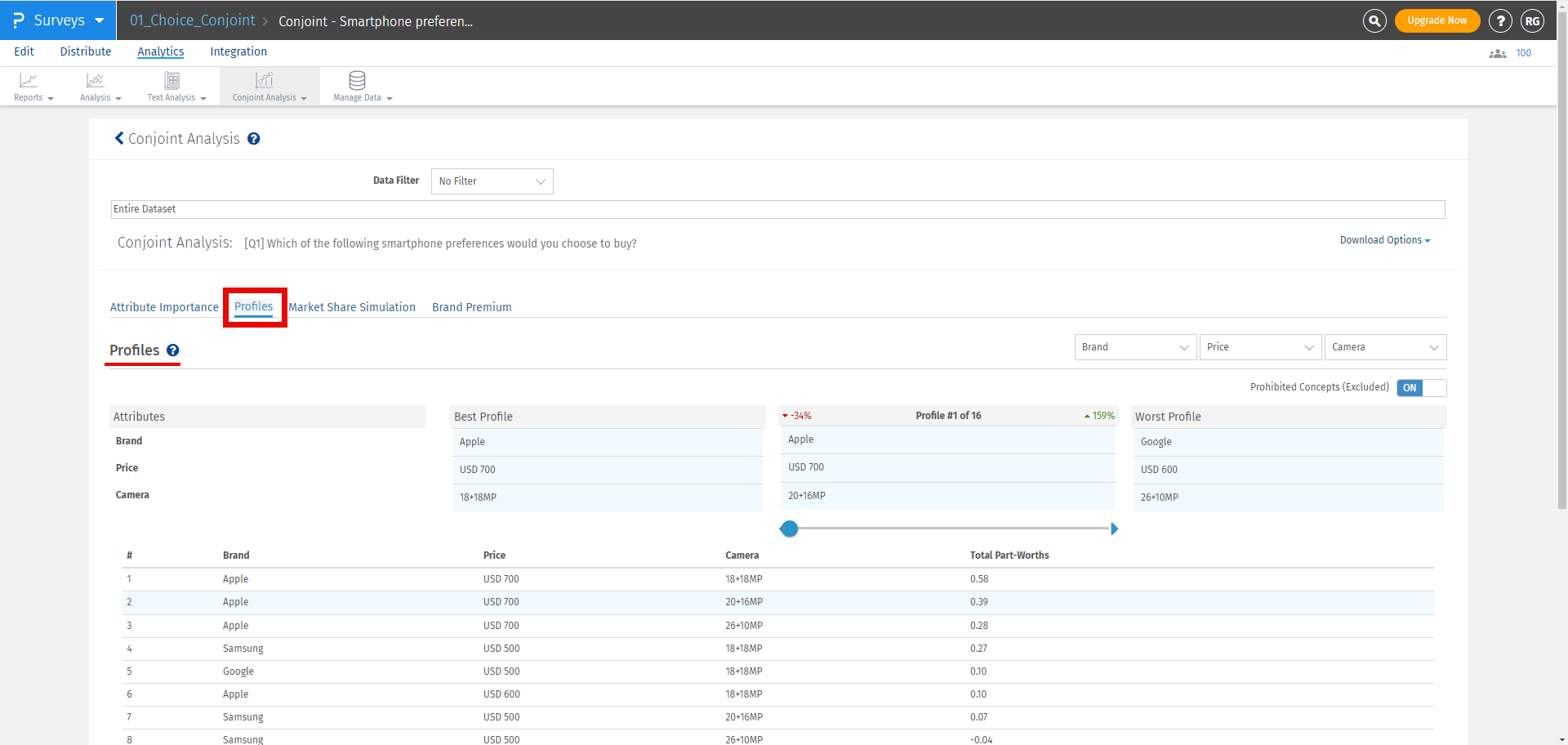 O melhor perfil é sempre exibido à esquerda e o pior perfil à direita. No meio, você pode selecionar um perfil personalizado para ver como ele se compara com o melhor e o pior perfil.
O melhor perfil é sempre exibido à esquerda e o pior perfil à direita. No meio, você pode selecionar um perfil personalizado para ver como ele se compara com o melhor e o pior perfil.
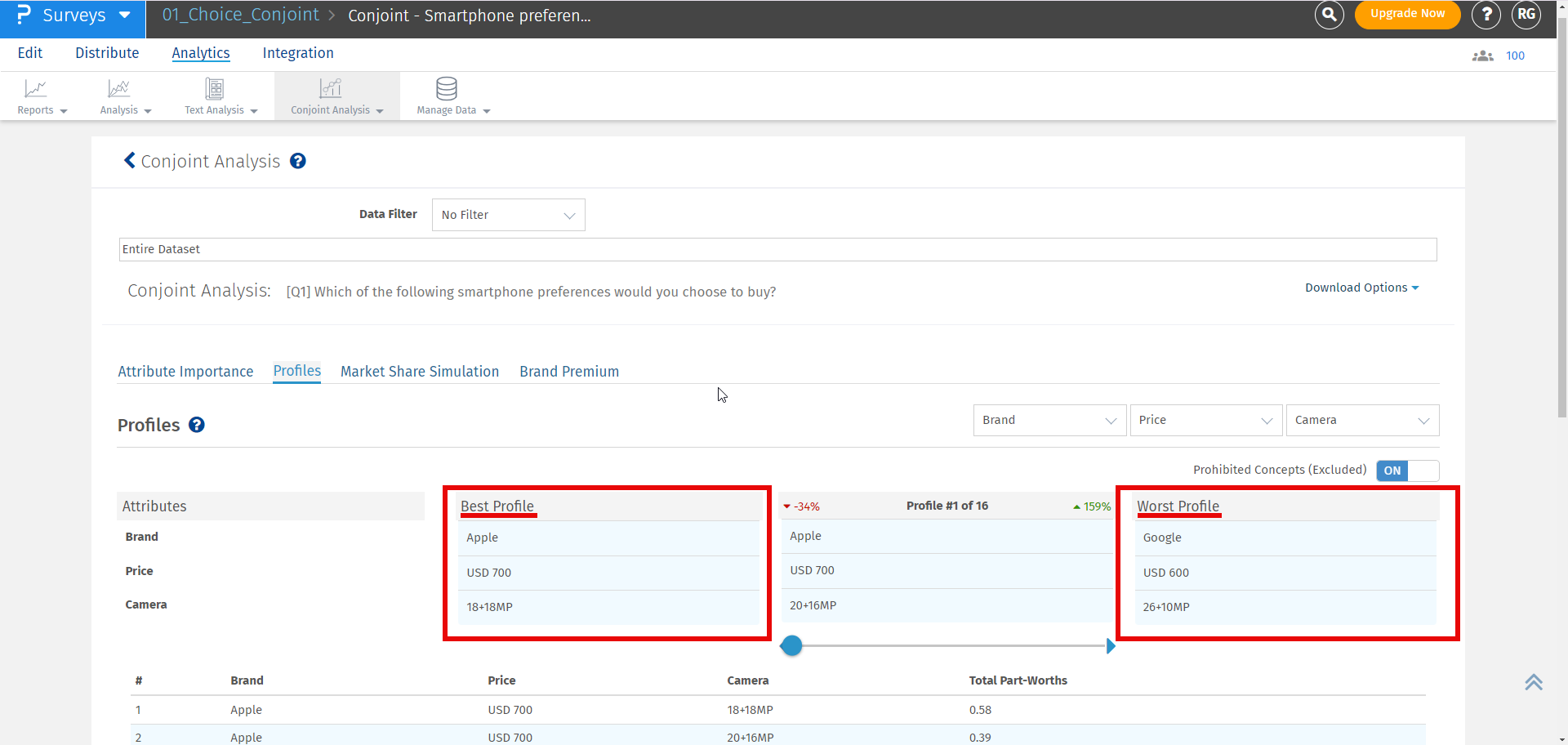 Se qualquer par for selecionado como par proibido, ele não será exibido no perfil melhor, pior ou personalizado. Se o usuário ainda quiser ver os pares proibidos, ele pode habilitar a opção de incluir pares proibidos.
Se qualquer par for selecionado como par proibido, ele não será exibido no perfil melhor, pior ou personalizado. Se o usuário ainda quiser ver os pares proibidos, ele pode habilitar a opção de incluir pares proibidos.
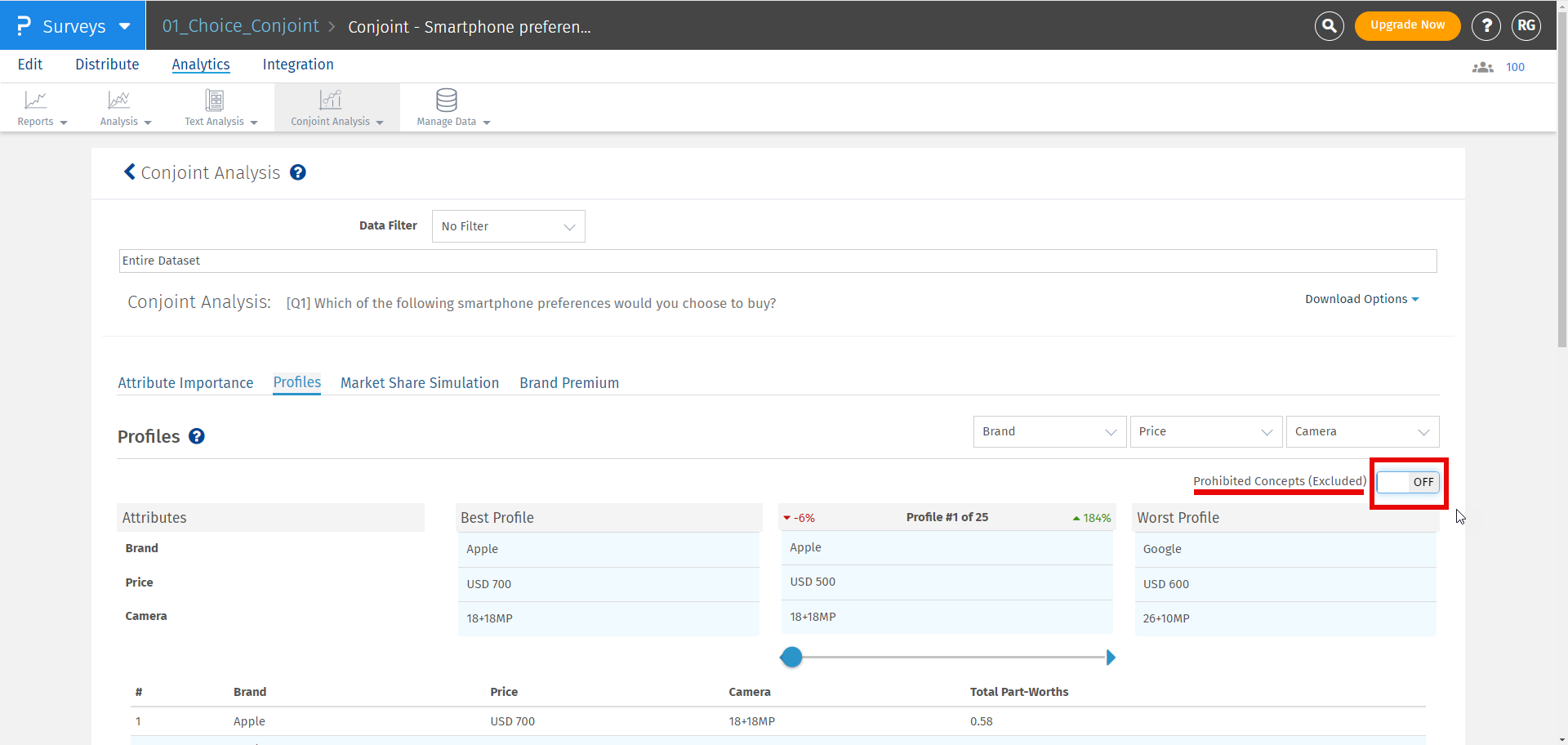 Para o perfil selecionado, você pode ver a diferença em pontos percentuais entre o melhor perfil e o perfil selecionado em vermelho. Por outro lado, a diferença em pontos percentuais entre o pior perfil e o perfil selecionado é exibida em verde.
Para o perfil selecionado, você pode ver a diferença em pontos percentuais entre o melhor perfil e o perfil selecionado em vermelho. Por outro lado, a diferença em pontos percentuais entre o pior perfil e o perfil selecionado é exibida em verde.
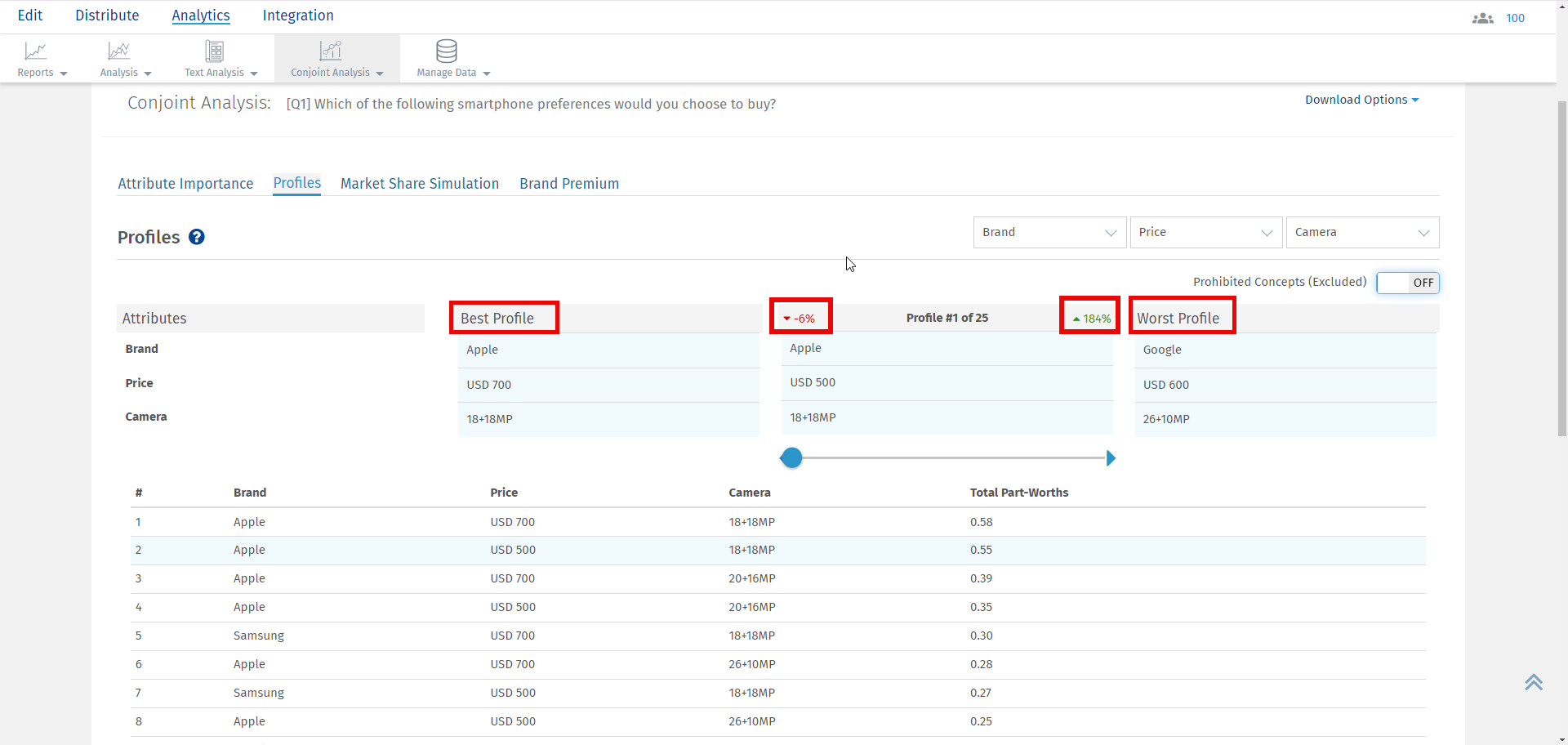 Nota: Atributo e nível com o maior Valor de Utilidade Parcial Total serão selecionados como o Melhor Perfil e aquele com o menor valor de Utilidade Parcial Total será selecionado como o Pior Perfil.
Nota: Atributo e nível com o maior Valor de Utilidade Parcial Total serão selecionados como o Melhor Perfil e aquele com o menor valor de Utilidade Parcial Total será selecionado como o Pior Perfil.
Usamos o seguinte algoritmo para calcular as Utilidades Parciais do Conjoint CBC:
Notação
Seja R o número de respondentes, com indivíduos r = 1 ... RSeja T o número de tarefas que cada respondente vê, com t = 1 ... T
Seja C o número de configurações (ou conceitos) que cada tarefa t tem, com c = 1 ... C (C em nosso caso é geralmente 3 ou 4)
Se temos A atributos, a = 1 a A, com cada atributo tendo La níveis, l = 1 a La, então a utilidade parcial para um atributo/nível específico é w’(a,l). É por esta (matriz irregular) de utilidades parciais que estamos resolvendo neste exercício.
Podemos simplificar isso para uma matriz unidimensional w(s), onde os elementos são:{w’(1,1), w’(1,2) ... w’(1,L1), w’(2,1) ... w’(A,LA)} com w tendo S elementos.
Uma configuração específica x pode ser representada como uma matriz unidimensional x(s), onde x(s)=1 se o nível/atributo específico estiver presente, e 0 caso contrário.
Seja Xrtc a configuração específica da c-ésima configuração na t-ésima tarefa para o r-ésimo respondente. Assim, o design do experimento é representado pela matriz de quatro dimensões X com tamanho RxTxCxS
Se o respondente r escolher a configuração c na tarefa t, então Yrtc=1; caso contrário, 0.
Utilidade de Uma Configuração Específica
A Utilidade Ux de uma configuração específica é a soma das utilidades parciais para os atributos/níveis presentes na configuração, ou seja, é o produto escalar x.wO Modelo Logit Multinomial
Para uma escolha simples entre duas configurações, com utilidades U1 e U2, o modelo MNL prevê que a configuração 1 será escolhidaEXP(U1)/(EXP(U1) + EXP(U2)) das vezes (um número entre 0 e 1).
Para uma escolha entre N configurações, a configuração 1 será escolhida
EXP(U1)/(EXP(U1) + EXP(U2) + ... + EXP(UN)) das vezes.
Probabilidade de Escolha Modelada
Seja a probabilidade de escolha (usando o modelo MNL) de escolher a c-ésima configuração na t-ésima tarefa para o r-ésimo respondente:Prtc=EXP(xrtc.w)/SUM(EXP(xrt1.w), EXP(xrt2.w), ... , EXP(xrtC.w))
Medida de Log-verossimilhança
A medida de Log-verossimilhança LL é calculada como:
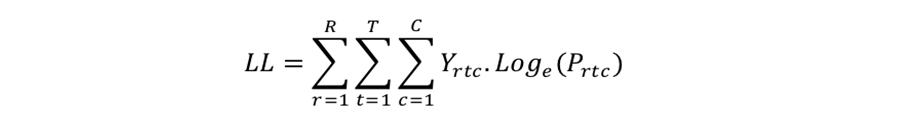
Prtc é uma função do vetor de utilidade parcial w, que é o conjunto de utilidades parciais que estamos resolvendo.
Resolvendo Para Utilidades Parciais Usando Máxima Verossimilhança
Resolvemos para o vetor de utilidade parcial encontrando o vetor w que dá o valor máximo para LL. Note que estamos resolvendo para S variáveis.Este é um problema de maximização contínua não linear multidimensional e requer uma biblioteca de solucionador padrão. Usamos o Algoritmo Simplex de Nelder-Mead.
A função de Log-verossimilhança deve ser implementada como uma função LL(w, Y, X) e, em seguida, otimizada para encontrar o vetor w que nos dá um máximo. As respostas Y e o design X são dados e constantes para uma otimização específica. Os valores iniciais para w podem ser definidos para a origem 0.
As utilidades parciais finais w são reescalonadas para que as utilidades parciais para qualquer atributo tenham uma média de zero, simplesmente subtraindo a média das utilidades parciais para todos os níveis de cada atributo.

